Fuzzy Logic Classification
Introducation
Currently the popular algorithms of hydrometeor classification are generally based on the fuzzy logic approach. It was first proposed by Vivekanandan et al. (1999) and tested on the S-Pol radar at the National Center for Atmospheric Research (NCAR). Later, many studies have improved the fuzzy logic classification with more complicated membership functions and decision criteria. Among them, there are two typical algorithms. One is the algorithm developed by the Colorado State University (CSU) (Liu et al. 2000, Lim et al. 2005) and has been transplanted in the commercial radars of Vaisala company. Unlike other algorithms that apply empirically derived membership functions, a notable feature of CSU algorithm is that its membership functions are trained in a neuro-fuzzy logic system. The other typical algorithm is the hydrometeor classification algorithm (HCA) developed by the National Severe Storms Laboratory (NSSL) (Ryzhkov et al. 2005, Schuur et al. 2003). This algorithm is primarily designed for the operation on the U.S. NEXRAD when the dual- polarization capacity is completely upgraded in 2012. The latest version was described by Park et al. (2009). It has been improved by accounting for the measurement error, beam broadening effect, the location of melting layer and the precipitation type (convective versus stratiform).
Fuzzy Logic Approach
The fuzzy logic classification generally has three steps. The first step is the fuzzification process. According to the statistics of polarimetric measurements, each radar echo class has a specific range of values for various polarimetric parameters. For the simplification and efficiency, appropriate membership functions are usually applied to characterize these ranges for the fuzzification. As shown in the following figure, the membership functions for rain and hail classes are defined by a trapezoidal function. The ranges of measurements, such as ZH, ZDR, ρhv and so on, are distinctly recognized for classes rain and hail. The overlapped region of two classes give a tolerance of possible inaccuracy of measurements. The next step is the aggregation process. In this step, the measurements are evaluated using membership functions. The cost function Ais applied to represent the total contribution of all the measurements, indicating how likely the input parameters result in an output class. For radar echo classification, the cost function normally has following form.
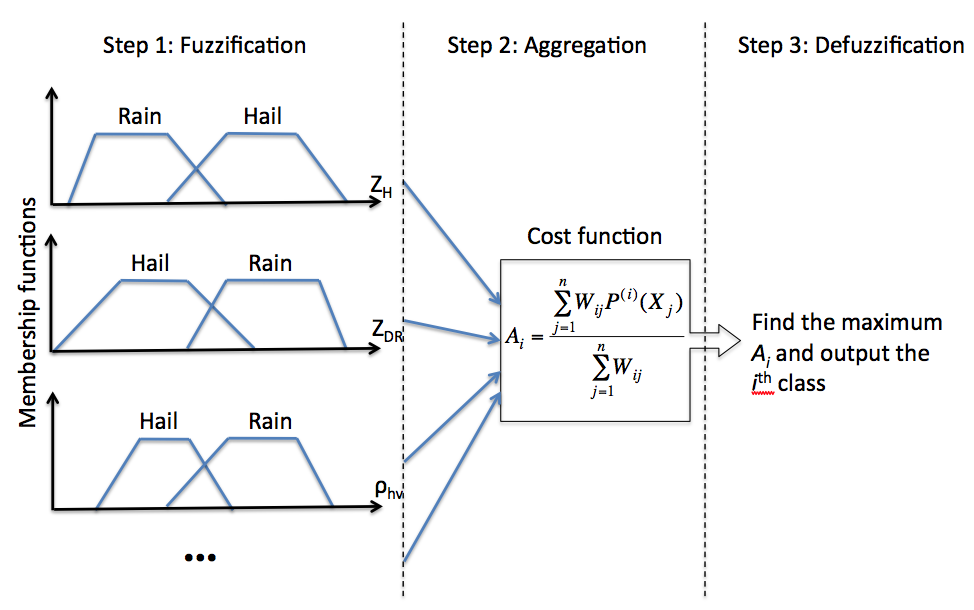
Illustration of fuzzy logic method using two example classes.
HCA
The major idea of the hydrometeor classification algorithm is to find the largest cost function for a specific class. As described in Park et al. (2009), a cost function of radar echo class is defined as follows.
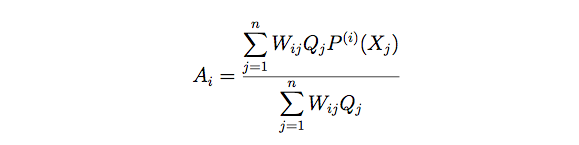
where, P(i)(Xj) is a membership function that characterizes the distribution of the jth radar variables Xj for the ith class; W denotes a weighting that represents the significance of radar variables for the classification; Q indicates a weighting associated with the data quality. The membership function P(X) generally has a form as shown in following figure.
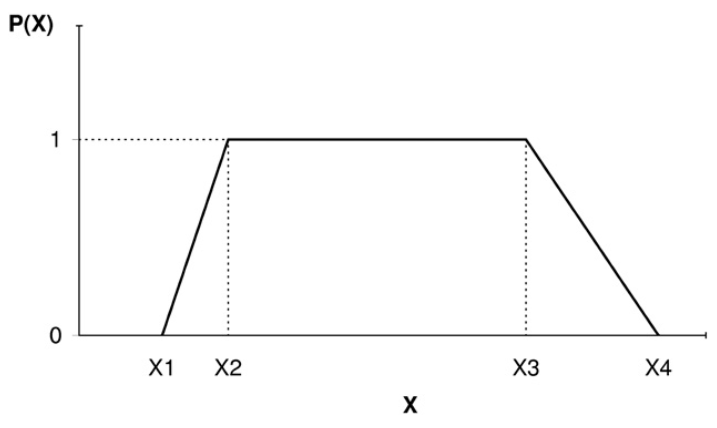
The Trapezoidal membership function, where X is an arbitrary polarimetric variable (from Park et al. 2009)
For a specific class, a polarimetric variable is assumed to have a value restricted within the range X1-X4. If the observation is beyond this range, the contribution of this variable is zero for the specific class. Otherwise, the weighting varies from 0 to 1, depending on which range the observation locates in. It worth noting that membership functions are major parts in a fuzzy logic algorithm. They make it possible to combine polarimetric observations in identifying the radar echo. Their control parameters (e.g., X1-X4) are generally found empirically or trained from verified observations.
Park et al. applied 6 parameters as input and output ten classes: GC/AP, BS, DS, WS, CR, GR, BD, RA, HR, and RH. These classes denote ground clutter/anomalous propagation, biological scatters, dry snow, wet snow, crystals, graupel, big drops, moderate rain, heavy rain and rain/hail mixture, respectively. The parameters for membership function is given by the following table.
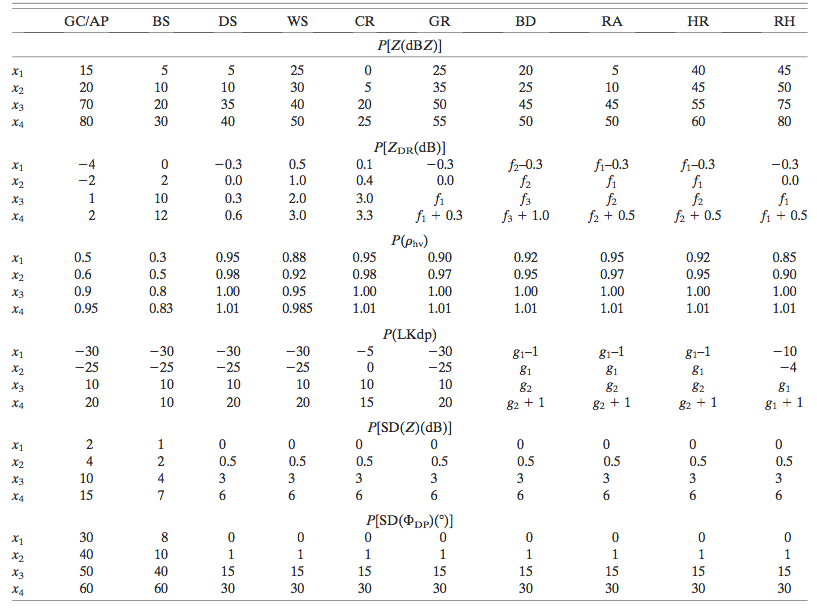
Parameters of the membership functions for 10 classes (from Park et al. 2009)
The weighting W in the cost function is given in the following talbe. It is seen that the contribution of each input parameter is different for various classes. The wighting Q associated with the data quality is a little complicated. Please refer to Park et al. (2009) for detialed description.
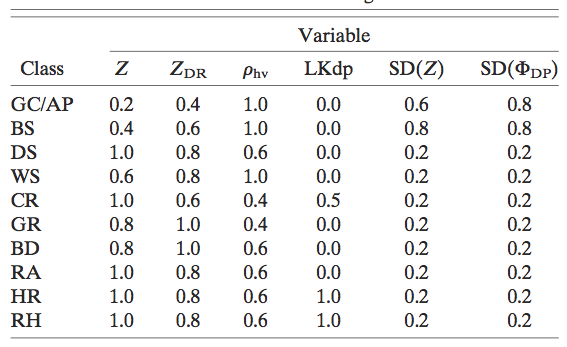
Significance weights of input parameters for 10 classes (from Park et al. 2009)
It is worth noting that there are some restricts for the classification according to the physical sense. It is dependent on the identification of melting layer. For example, below the melting layer there should not include snow, crystal, and graupel classes while there should not have classes of pure rain, clutter and biological scatterers above the melting layer. Park's creiterion for the decision is shown as follows when melting layer is identified.
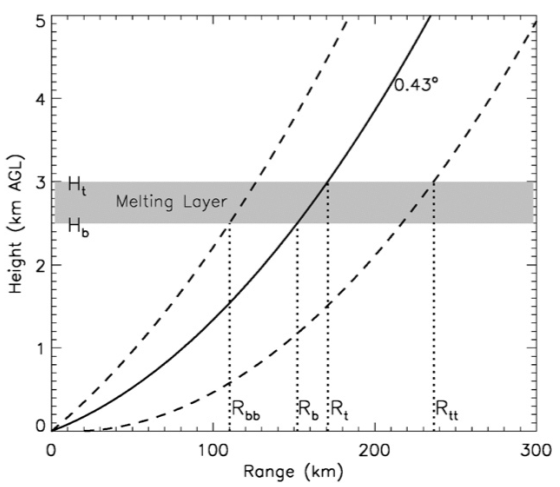
Geometry of the radar beam with respect to the melting layer (from Park et al. 2009)
- 0 <Range <Rbb-GC/AP, BS, BD, RA, HR, RH;
- Rbb <Range <Rb-GC/AP, BS, WS, GR, BD, RA, HR, RH;
- Rb <Range <Rt-GC/AP, BS, DS, WS, GR, BD, RH;
- Rt <Range <Rtt-GC/AP, BS, DS, WS, CR, GR, BD, RH;
- Range >Rtt-DS, CR, GR, RH.
Study Module
Objectives
- To understand the characteristics of polarimetric radar variables for different types of scatterers.
- To learn the use of fuzzy logic approach for classification issues.
- To strengthen the knowledge of physical structure in a storm and corresponding radar measurements.
Description
The task of this module is to classify radar echoes using a fuzzy logical algorithm. The classification
scheme in this module is similar to the latest studies of Park et al. (2009)
but has been simplified. For example, The membership functions have been reduced to three polarimetric
variables. The significance for different polarimetric variables and the data quality are not considered.
The weighting functions W and Q in equation 1 are assumed to be 1. However, the approach in this module
is easy to understand and follow for the readers.
This module applies three radar measurements ZH,
ZDR, and ρhv as the input. The radar echo is identified with ten classes:
1) ground clutter or abnormal propagation (GC/AP); 2) biological scatterers (BS); 3) dry aggregated snow (DS);
4) wet snow (WS); 5) crystals (CR); 6) graupel (GR); 7) big drops (BD); 8) light and moderate rain (RA);
9) heavy rain (HR), and 10) a mixture of rain and hail (HA). There are some restricts according to the
location of melting layer (Schuur et al. 2003). For the region
below the melting layer, only class GC/AP, BS, BD, RA, HR, and HA are allowed. For the region above the
melting layer, only GC/AP, CR, GR, and HA are classified. For the region within the melting layer, only
GC/AP, BS, DS, WS, GR, BD, and HA are output. The parameters of the membership function are listed in the
following table for every combination of the class and radar variable.
Procedures
- Download ZH, ZDR, and ρhv data following the link.
- According to equation 1 and membership functions listed in table \ref{tab:class}, calculate the cost function for each class.
- Do the classification based on the calculated cost functions as well as the melting layer criterion.
- Plot the radar measurements and the classification results. Check and interpret the classification using a common sense of the storm physics.