DSD Retrieval from Radar Data
DSD models
A DSD model is required for the DSD retireval. The following DSD models are generally used.

- M-P model is a single parameter model with a slope parameter Λ. This well-known model was proposed by Marshall and Palmer (1948) and was widely used in the past 50 years. It was helpful in bulk-scheme rain parameterization and radar-rain estimation.
- Exponential model has two parameters: a concentration parameter N0 and Λ. It is more flexible than M-P model since the latter is equivalent to the exponential model with a fixed N0.
- In addition to N0 and Λ, gamma distribution introduces a shape parameter μ. It has been widely accepted that the gamma model is flexible to represent the variability of natural DSDs.
- Gamma DSD is sometimes applied with its normalized form (e.g., Bringi et al. 2002). Nw is a normalized parameter, the value of which equals to the intercept parameter of an exponential DSD that has the same water content and the median volume diameter D0.The advantage of a normalized gamma DSD is that parameters (Nw and D0) have specific physical meaning.
- For log-normal distribution, NT is the total number concentration. η and σ are the mean and standard deviation of Gaussian distribution, respectively. This model follows the assumption that parameters of the DSD can be modeled as random variables from a multivariate Gaussian distribution. It has a good explanation of DSD based on the probability theory, and the mathematical calculation is not that complicated. However, it might not be the best one matching observed DSDs.
-
The constraint-gamma (C-G) DSD modole was recently proposed by
Zhang et al. (2001). With the correlation
between μ and Λ, it reduces the gamma DSD to a two-parameter model. It facilitates the DSD
retrieval from two radar observations while still keeps a good flexibility to represent natural DSDs. The
latest C-G was updated using rain date observed by disdrometer in central Oklahoma
(Cao et al. 2008) as
μ = -0.0201Λ2 + 0.902Λ -1.718
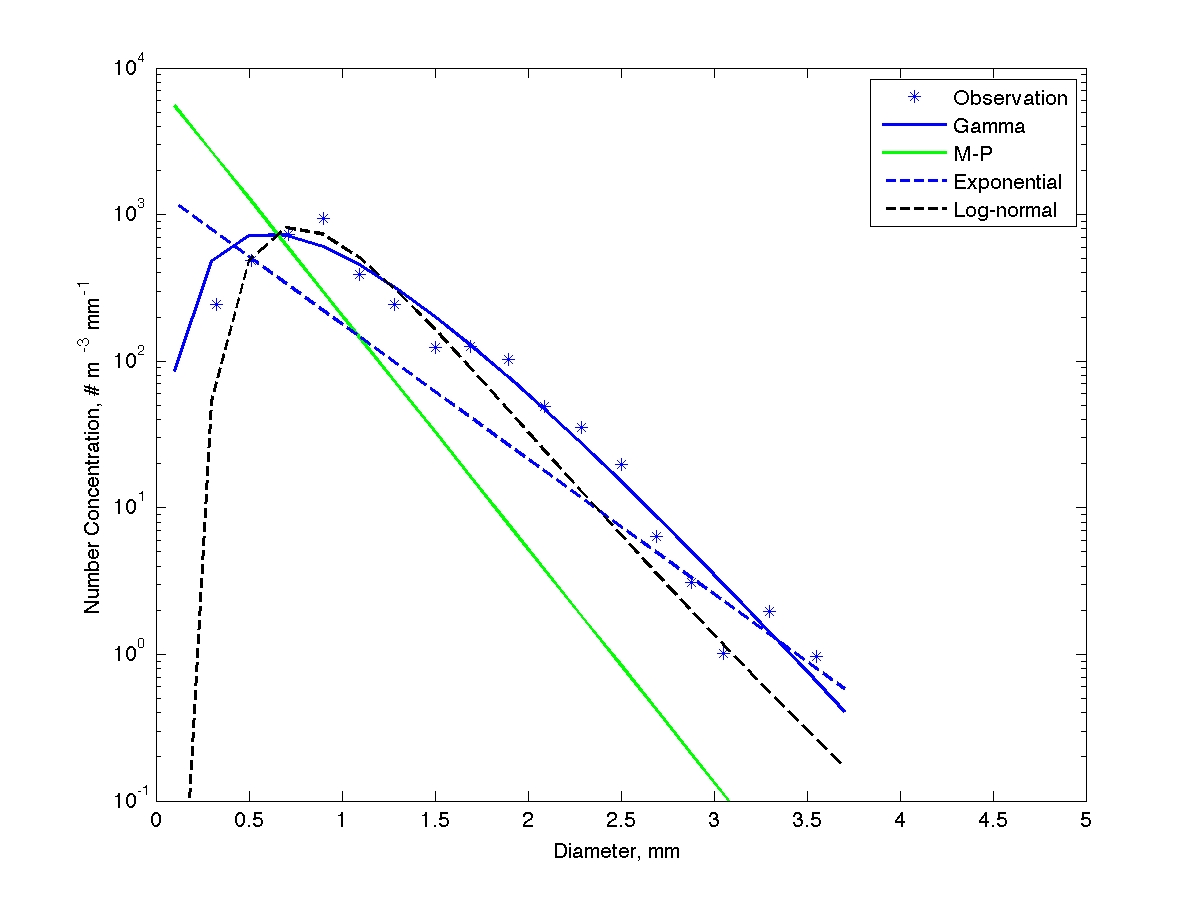
Example of an disdrometer-observed DSD, which is represented by different DSD models.
Above figure shows an example of DSD models representing an observed DSD. It is evident that the M-P model has the worst performance. The DSD model, which has more freedom (i.e., more parameters), represent the observation better. The observed DSD in the figure is well modeled by the gamma function.
Retrieval Methods
Generally, the retrieval procedure is to find a DSD, based on which the calculated radar variables could match the
radar observations. This fact implies that the calculation of radar variables should be a key factor to the DSD
retrieval because it connects the DSD to the radar variables. The method of calculating radar variables is usually
called the forward operator, which has designated the DSD model, the raindrop shape model, and other conditions
for the scattering such as frequency and temperature. It is worth noting that the forward operator of radar
variables could not reflect the real radar observations accurately. There would exist representing errors, which
could affect the performance of DSD retrieval. These errors, including DSD model error and raindrop shape model
error, can be viewed as the model error.
The straightforward way of DSD retrieval is to solve the unknown DSD parameters using the same number of radar
observations. For example, if the exponential DSD model is used for the retrieval, two parameters N0
and Λ need to be solved. If there are two observations ZH and ZDR available, we
can use forward operators of ZH and ZDR, to solve these two DSD parameters. This approach
assumes the forward operator results exactly match the observations and the DSD parameters are deterministically
solved. The limitation is that the observation and model errors are not considered in this approach. Regardless
of its defects, the direct DSD retrieval is convenient to be applied. It has been demonstrated with a good performance
when an appropriate DSD model is used (Brandes et al. 2004,
Zhang et al. 2006,
Cao et al. 2008).
Other methods for the DSD retrieval work on the use of additional information for the optimization of retrieval.
For example, the variational approach (Xue et al. 2009, Cao et al. 2009) provides a good way to combine multiple
radar observations and spatial information to retrieve the DSD with minimizing the observation error effects.
The long-term statistics of rain properties can also be used to improve the DSD retrieval
(Cao et al. 2010).
Although these methods are more complicated than the direct retrieval, their basses are same, i.e., they are
primarily based on the forward operator.
Study Module
Objectives
- To enhance the understanding of DSD and its relation with different rain variables.
- To learn the method of retrieving DSD from radar measurements.
- To gain the knowledge of the difference between DSD models and their impacts on the rain retrieval.
Description
This module gives a practice of DSD retrieval using the direct approach. In brief, the retrieval uses two radar measurements ZH and ZDR to solve two unknown DSD parameters. Two DSD models are compared for the retrieval. One is the exponential model. The other is the C-G model. Both models are two-parameter based.
Procedures
- Download the example radar data ZH, and ZDR following the link.
- Assuming the DSD follows the exponential form, solve parameters N0 and Λ from observed ZH and ZDR according to equations 1 and 2.
- Repeat this retrieval but use a C-G DSD model.
- Calculate rainfall rate and mean volume diameter using equations of R and Dm, respectively.
- Plot and analyze the results of N0, Λ R, and Dm. Compare the retrieval results using different DSD models.